| Yves Herman/Reuters | ||
 | ||
| Imagem de Napoleão feita com Lego |
Napoleão Bonaparte foi um dos maiores generais e estrategistas da história. Foi também o governante e estadista que reconstruiu o estado francês dos escombros da revolução de 1789, fazendo da França a maior potência do seu tempo. O que é menos sabido é que Napoleão também foi um matemático e cientista praticante, imerso nos avanços científicos de sua época e totalmente consciente de sua importância para o desenvolvimento do país.
As anedotas do seu tempo na escola militar o descrevem como excelente aluno e extremamente ambicioso. Uma delas conta que o professor e grande matemático Laplace passou o "Traité de mathématiques" de Bézout, com seus 4 espessos volumes, para os alunos estudarem em dois anos. Sabendo que a matemática era indispensável nos exames para promoção, Napoleão focou-se totalmente nessa tarefa, deixando de lado matérias como o latim, o alemão, a gramática e a ortografia.
Valeu a pena: apenas um ano depois, aos 16 anos, já era oficial de artilharia. Aos 24, seria general.
Napoleão manteve o interesse pela matemática e pela ciência ao longo da vida. É um raríssimo caso de governante que também foi membro da academia de ciências de seu país (o Institut de France), participando ativamente nas sessões.
Apenas dois dias após tomar o poder na França, por meio do golpe de estado de 18 de Brumário, compareceu normalmente à academia para apresentar um trabalho intitulado "Memória sobre as equações às diferenças misturadas". Para evitar constrangimentos assinou, simplesmente, como cidadão Bonaparte.
Continuou apaixonado pela matemática e participando nos trabalhos da academia por um longo período, embora a frequência fosse diminuindo à medida que aumentavam suas responsabilidades como governante.
Em 1802, escreveu a seu ex-professor Laplace: "Vivo a tristeza de não poder dedicar [ao estudo da Matemática] o tempo e a atenção que ele merece. É mais uma ocasião para me afligir com a força das circunstâncias que me conduziram para outra carreira, onde me encontro tão longe da carreira das ciências".
Outra história conta que, nas noites precedendo as grandes batalhas, Napoleão relaxava resolvendo problemas de geometria. Para mim, faz todo o sentido: já fiz exatamente o mesmo, ainda que em circunstâncias menos dramáticas.
Talvez o lindo Teorema de Napoleão seja o resultado de uma dessas vigílias antes da batalha; não sabemos: ignoramos até se ele é realmente de autoria do imperador ou lhe foi atribuído por alguém que queria tornar o teorema mais "interessante". Seja como for, os leitores merecem conhecer essa pequena maravilha matemática.
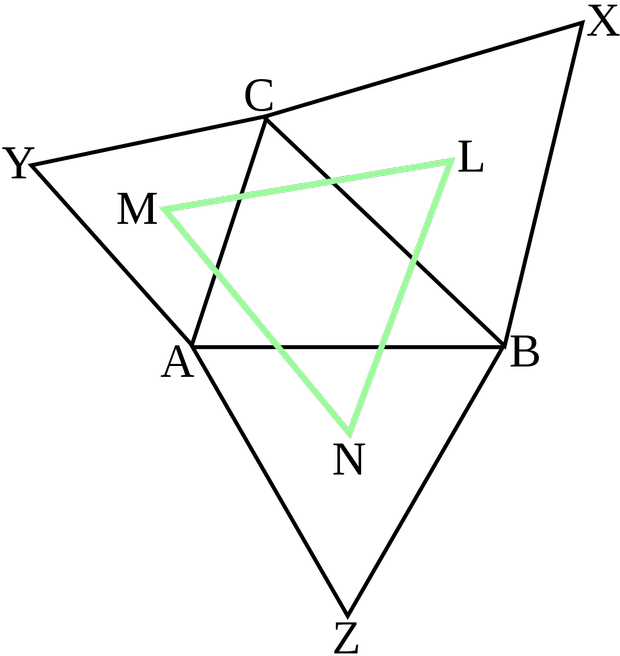
Considere um triângulo qualquer ABC. Desenhe 3 triângulos equiláteros (com três lados de igual comprimento), como indicado na figura: cada um deles tem um lado em comum com o triângulo ABC. Agora considere o triângulo LMN formado pelos centros desses três triângulos ACY, BAZ e CBX. O Teorema de Napoleão diz que esse triângulo LMN é sempre equilátero: não importa a escolha do triângulo ABC, os três lados do triângulo LMN têm o mesmo comprimento.
Em outra carta a Laplace, de 1812, em plena invasão da Rússia, Napoleão escreveu que "o avanço e a perfeição da matemática estão intimamente ligados à prosperidade do Estado".
As campanhas napoleônicas viraram a Europa de pernas para o ar, causaram milhares de mortes e foram determinantes até para a história do Brasil. Para alguns, ele foi um agressor sanguinário e um tirano, para outros um gênio militar e um estadista sem igual.
De todo o seu legado, talvez o mais importante seja a ideia –nova no seu tempo– de que uma nação que se quer forte e próspera precisa de uma verdadeira política científica.
Duzentos anos depois, é hora de o Brasil aprender essa novidade.
As anedotas do seu tempo na escola militar o descrevem como excelente aluno e extremamente ambicioso. Uma delas conta que o professor e grande matemático Laplace passou o "Traité de mathématiques" de Bézout, com seus 4 espessos volumes, para os alunos estudarem em dois anos. Sabendo que a matemática era indispensável nos exames para promoção, Napoleão focou-se totalmente nessa tarefa, deixando de lado matérias como o latim, o alemão, a gramática e a ortografia.
Valeu a pena: apenas um ano depois, aos 16 anos, já era oficial de artilharia. Aos 24, seria general.
Napoleão manteve o interesse pela matemática e pela ciência ao longo da vida. É um raríssimo caso de governante que também foi membro da academia de ciências de seu país (o Institut de France), participando ativamente nas sessões.
Apenas dois dias após tomar o poder na França, por meio do golpe de estado de 18 de Brumário, compareceu normalmente à academia para apresentar um trabalho intitulado "Memória sobre as equações às diferenças misturadas". Para evitar constrangimentos assinou, simplesmente, como cidadão Bonaparte.
Continuou apaixonado pela matemática e participando nos trabalhos da academia por um longo período, embora a frequência fosse diminuindo à medida que aumentavam suas responsabilidades como governante.
Em 1802, escreveu a seu ex-professor Laplace: "Vivo a tristeza de não poder dedicar [ao estudo da Matemática] o tempo e a atenção que ele merece. É mais uma ocasião para me afligir com a força das circunstâncias que me conduziram para outra carreira, onde me encontro tão longe da carreira das ciências".
Outra história conta que, nas noites precedendo as grandes batalhas, Napoleão relaxava resolvendo problemas de geometria. Para mim, faz todo o sentido: já fiz exatamente o mesmo, ainda que em circunstâncias menos dramáticas.
Talvez o lindo Teorema de Napoleão seja o resultado de uma dessas vigílias antes da batalha; não sabemos: ignoramos até se ele é realmente de autoria do imperador ou lhe foi atribuído por alguém que queria tornar o teorema mais "interessante". Seja como for, os leitores merecem conhecer essa pequena maravilha matemática.
Considere um triângulo qualquer ABC. Desenhe 3 triângulos equiláteros (com três lados de igual comprimento), como indicado na figura: cada um deles tem um lado em comum com o triângulo ABC. Agora considere o triângulo LMN formado pelos centros desses três triângulos ACY, BAZ e CBX. O Teorema de Napoleão diz que esse triângulo LMN é sempre equilátero: não importa a escolha do triângulo ABC, os três lados do triângulo LMN têm o mesmo comprimento.
 | ||
As campanhas napoleônicas viraram a Europa de pernas para o ar, causaram milhares de mortes e foram determinantes até para a história do Brasil. Para alguns, ele foi um agressor sanguinário e um tirano, para outros um gênio militar e um estadista sem igual.
De todo o seu legado, talvez o mais importante seja a ideia –nova no seu tempo– de que uma nação que se quer forte e próspera precisa de uma verdadeira política científica.
Duzentos anos depois, é hora de o Brasil aprender essa novidade.


Nenhum comentário:
Postar um comentário